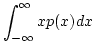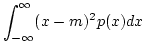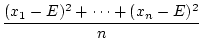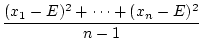

Next: 公式集
Up: まとめ
Previous: まとめ
- 有効数字
- 数の標記から位取りをあらわすための0を取り除いた有意義な桁数の数字のこと。
- 真の値
- 測定量の正しい値。特別な場合を除き, 観念的な値で,
実際には求められないので, 真の値とみなしうる値を用いることがある。
- 最良推定値
- 最も良いと思われる推定値。
- 誤差
- 測定値から真値とみなしうる値(多くの場合は最良推定値)
を引いた値。より曖昧に, 測定値に含まれる不確かな部分の意味で用いられることもある。
- 偶然誤差
- 突き止められない原因によって起こり, 測定値のばらつきとなって現れる誤差。
- 系統誤差
- 測定値にかたよりを与える原因によって生じる誤差。
- 相対誤差
- 誤差と最良推定値の比率。 誤差率。
- 誤差率
- 相対誤差と同じ。
- 間接測定
- 測定したい量と一定の関係にあるいくつかの量について計測をおこない,
その計測値から測定したい量を求めること。
- 確率変数
- その取り得る値が確率的に決まるような変数。
- 確率分布関数
- 確率変数が
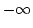 から
から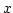 までの値を取る確率を縦軸に,
までの値を取る確率を縦軸に,
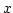 の値を横軸に取ったグラフによってあらわされる関数。
の値を横軸に取ったグラフによってあらわされる関数。
- 確率密度関数
- 確率分布関数の導関数。
- 正規分布
- 確率密度関数が
![$\displaystyle \frac{1}{\sqrt{2 \pi}\sigma}\exp[-\frac{(x-m)^2}{2 \sigma^2}]$](img141.png) で与えられる確率分布。
で与えられる確率分布。
- 確率的に独立
- 2個の確率変数
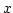 と
と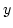 に対し,
に対し, 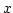 がどのような値を取ったときにも,
がどのような値を取ったときにも,
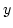 が特定の値を取る確率が変わらないとき,
が特定の値を取る確率が変わらないとき, 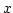 と
と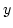 は確率的に独立であるという。
は確率的に独立であるという。
- 平均
- 確率変数
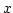 およびその確率密度関数
およびその確率密度関数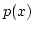 に対し,
によって定義される量。
に対し,
によって定義される量。
- 分散
- 確率密度関数
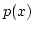 および平均
および平均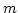 を持つ確率変数
を持つ確率変数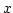 に対し,
によって定義される量。
に対し,
によって定義される量。
- 標本平均
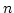 個の標本
個の標本
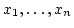 に対し
によって定義される量。
に対し
によって定義される量。
- 標本分散
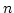 個の標本
個の標本
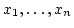 に対し
によって定義される量
(
に対し
によって定義される量
(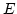 は標本平均)。
は標本平均)。
- 不偏分散
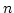 個の標本
個の標本
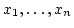 に対し
によって定義される量
(
に対し
によって定義される量
(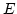 は標本平均)。
は標本平均)。
- 尤度関数
- 確率分布のパラメータ
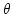 と標本
と標本
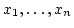 に対し,
組
に対し,
組
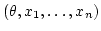 がしたがう確率分布の確率密度関数のことを
尤度関数とよぶ。
がしたがう確率分布の確率密度関数のことを
尤度関数とよぶ。
- 不偏推定量
- その期待値がパラメータの真値
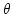 に一致するような推定量。
に一致するような推定量。
- 最尤推定量
- 与えられた観測値のもとで尤度関数が最大となるような値を
パラメータ推定値としたもの。


Next: 公式集
Up: まとめ
Previous: まとめ
Shigeru HANBA
平成16年8月16日
![$\displaystyle \frac{1}{\sqrt{2 \pi}\sigma}\exp[-\frac{(x-m)^2}{2 \sigma^2}]$](img141.png) で与えられる確率分布。
で与えられる確率分布。
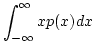
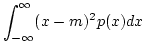
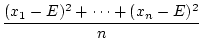
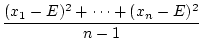
![$\displaystyle \frac{1}{\sqrt{2 \pi}\sigma}\exp[-\frac{(x-m)^2}{2 \sigma^2}]$](img141.png) で与えられる確率分布。
で与えられる確率分布。